12. Anchorage Zone

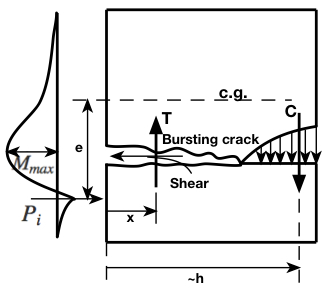
At the anchorage zones for prestressed members (whether pre-tensioned or post-tensioned), there are stress concentrations which can cause unusual stress patterns. There are three different methods for evaluating anchorage zones.

Approximate elastic design (empirical):

For $\frac{h_b}{h} < 0.2$ ,

(1) $\begin{equation*} T = 0.3P\left(1-\frac{h_b}{h}\right)\end{equation*}$

$h_b =$ depth of bearing plate

$h =$ depth of member

For $\frac{h_b}{h} > 0.2$ ,

(2) $\begin{equation*} T = 0.25P\left(1-\frac{h_b}{h}\right)\end{equation*}$

$T =$ tension force in the ‘bursting’ zone

The resultant tensile force in the ‘spalling’ zone above the tendon is about $.02P$ (empirical)

e.x.

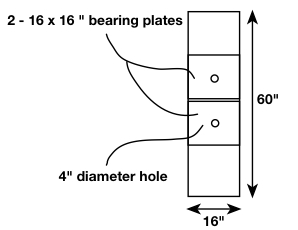
Each tendon consists of $14 \frac{1}{2}in$ diameter low-relaxation strands with $f_{pu} = 270 ksi$ , stressed to $0.75f_{pu}$ , $f'_{ci}=5000 psi$ mild reinforcement $f_y= 60 ksi$

Check the bearing stresses under the anchor plates:

$P = 14 * .153 * .75 * 270 = 434 kips$

Net bearing area of each plate:

$A = 16*16 - \frac{\pi*4^2}{4} = 243 in^2$

$\frac{P}{A} = \frac{434}{243} = 1.79 ksi$ , which is about $0.36 f'_{ci} \therefore \text{ OK}$

We can treat the two bearing plates as a single bearing plate with bearing area $16x 32''$ , and subjected to a tendon force of $2*434 = 868 kips$

(3) $\begin{equation*} \frac{h_b}{h} = 0.53 \Rightarrow T = 0.25*868*(1-\frac{32}{60}) = 101kips \end{equation*}$

In order to keep the stress in the reinforcement below $.5f_y = .5*60 = 30 ksi$ , the minimum total stirrup area, required in the ‘bursting’ zone, is:

$A_s = \frac{101}{30} = 3.37in^2$

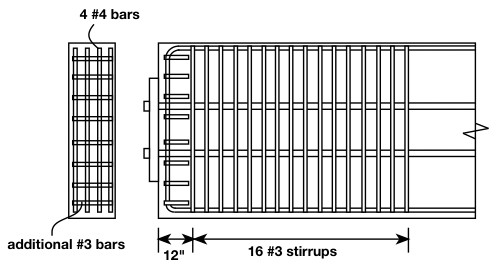
How many #3 stirrups is this?

$\frac{3.37}{2*0.11} = 15.3$ stirrups

We can use 16 stirrups, spaced at 3.5”, with the first stirrup at 12” from the end face.

In order to control ‘spalling’, we need to resist a tensile force of $.02P = .02*868 = 17.36 kips$ .

$A_s = \frac{17.36}{30} = 0.58in^2$

How many #4 bars is this?

$\frac{0.58}{(0.2)} = 2.9 bars$ (note that these could be straight bars as opposed to U-shaped stirrups)

We can conservatively use 4 bars.

Additional #3 bars will be used at the end face for confinement.

Importance of proper stirrup spacing in anchorage zones:

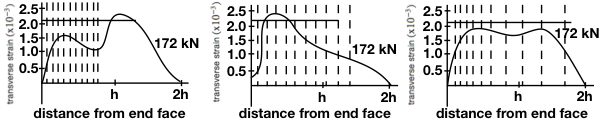
We want to avoid the situation on the far left. The far right is ideal. The middle is acceptable, and is the easiest to implement.

Linear Elastic Stress design:

e.x.

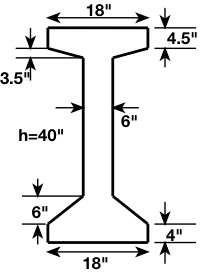
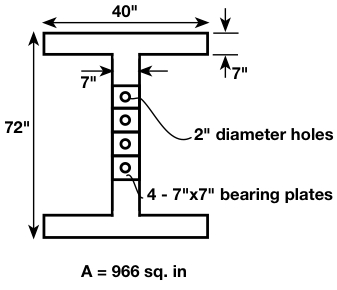
Design the end anchorage reinforcement for the post-tensioned beam shown below, which spans $L =65'$

$f'_c = 5000 psi$
$P_i = 376110 lb$
$c_b = 18.84in$
$e = 12.49in$
$A = 377 in^2$
$I = 70688 in^4$

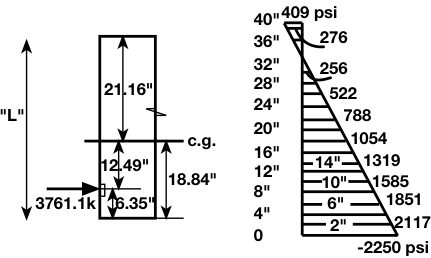
Distance of tendon (or centroid of tendons) from the bottom fiber:

$18.84 - 12.49 = 6.35''$

Within the anchorage zone, the span to depth ratio is small enough, that we basically have something analogous to a beam of length $``L''$ shown below. Recall from statics, that the internal bending moment can be found from the ‘cutting’ method. This moment can be found from either the left FBD or the right FBD. In our case, our ‘beam’ can be thought of as resting flat on the ground and our FBD is to choose from are either top or bottom rather than left or right. We will choose bottom.

The concrete internal moment at the plane 4” from the bottom fibers:

(4) $\begin{equation*} M_{c4} = 2117*4*18*(2") = 304848in*lb = 0.3 \text{x} 10^6 in*lb\end{equation*}$

The concrete internal moment at the plane 8” from the bottom fibers:

(5) $\begin{equation*} M_{c8} = 2117*4*17*6" + 1841*4*\frac{18+10}{2}*2" = 1121856in*lb = 1.12 \text{x} 10^6 in*lb\end{equation*}$

We’re using width $\frac{18+10}{2}$ since this is the average width between $4''$ from the bottom fiber and $8''$ from the bottom fiber.

The prestressing force moment at the plane $8''$ from the bottom fibers is

(6) $\begin{equation*} M_{c8} = 376110*(8-6.35) = -620582 = -0.62 \text{x} 10^6 in*lb\end{equation*}$

The net moment is then $1.12 \text{x} 10^6 - .62 \text{x} 10^6 = .50 \text{x} 10^6 in*lb$

We can repeat this procedure throughout the height of the beam to obtain the maximum positive and negative moments.

Moment plane distance 'd' from the bottom $(in)$	Section width $(in)$	Moment from tendon about the horizontal plane of interest $(in*lb\text{x} 10^6)$	Moment from concrete about the horizontal plane of interest $(in*lb \text{x} 10^6)$	Net moment $(in*lb \text{x} 10^6)$
0	18	0	0	0
4	18	0	0.30	0.30
6.35	13.3	0	0.75	0.75
8	10	-0.62	1.12	0.50
12	6	-2.14	2.25	0.12
16	6	-3.63	3.54	-0.09
20	6	-5.13	4.94	-0.19
24	6	-6.64	6.44	-0.20
28	6	-8.14	7.99	-0.15
32	6	-9.65	9.61	-0.04
36	18	-11.15	11.13	-0.02
40	18	-12.66	12.66	0

We can take $x$ to be $15''$ here and conservatively ignore any resistance to tension from the concrete itself. It is important to note that this is very conservative and can also give the misleading impression that wider anchorage zones actually adversely effect anchor zone reinforcement, which we know not to be true.

Bursting zone:

(7) $\begin{equation*} T = \frac{M_{max}}{h-x} = \frac{0.75\text{x}10^6}{40-15}=30000 lb \end{equation*}$

Take $f_s = 20000 psi$ (code allows $0.6f_y = 360000psi$ )

(8) $\begin{equation*} A_s = \frac{T}{f_s} = \frac{30000}{20000} = 1.5in^2 \end{equation*}$

Spalling zone:

(9) $\begin{equation*} T = \frac{-2\text{x}10^6}{40-15} = 8000 lb\end{equation*}$

where $-2\text{x}10^6in*lb$ is the largest negative moment

(10) $\begin{equation*} A_s = \frac{T}{f_s} = \frac{8000}{20000} = 0.40 in^2 \end{equation*}$

Stirrups can then be proportioned as appropriate

Strut-and-Tie design:

e.x.

Each tendon consists of $\frac{1}{2}"$ diameter low-relaxation strands, stressed to $.75$ , where

$f_{pu} = 270 ksi$

$f'_{ci} = 5000 psi$

Post-tensioned anchorage zones must be designed to withstand the ultimate tensile force of the tendons:

For each tendon:

$P = 4*.153*270 = 165 kips$ (4 strands per tendon)

Compressive stresses:

Net bearing area of each plate:

(11) $\begin{equation*} A = 7*7 - \frac{\pi*2^2}{4} = 45.9 in^2\end{equation*}$

Bearing stress $= \frac{165}{45.9} = 3.60 ksi$

where $165 kips$ is the force from one tendon

Permissible nodal stress limit:

(12) $\begin{equation*} 0.85\phi f'_{ci} = 0.85*0.90*5 = 3.83 ksi \therefore \text{ OK}\end{equation*}$

Outside of the immediate bearing region, the compressive stress can be idealized as uniform:

(13) $\begin{equation*} f_c = \frac{4*165}{966in^2} = .683 ksi \end{equation*}$

This results in a compressive force of $.683*40''*7'' = 191 kips$ , in each flange, and $277 kips$ in the web

The total bearing force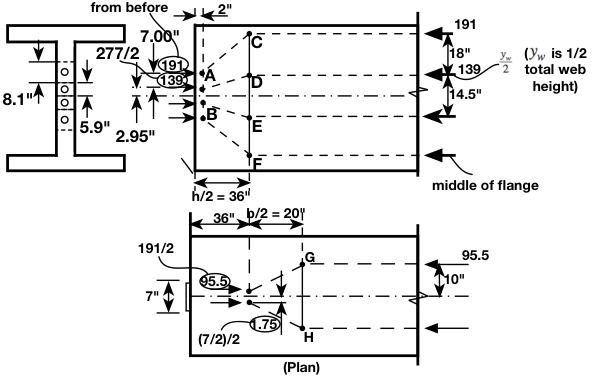 $4*165 = 660 kips$ can be distributed, using the strut-and-tie model shown:

The total bearing plate height is in fact $28''$ , but the holes are not necessarily drilled in the center of each plate.

Member	CD = EF	DE	GH
Force in kips	127.6	173.9	39.4

If #4 stirrups are used $(f_y = 60 ksi)$ , each stirrup has a factored tensile resistance of $</i><i>.9*60*.40 = 21.6 kips$

since $F_{DE}$ governs, $\frac{173.9}{21.6} = 8.1$ stirrups

$\rightarrow$ Use 9 – #4 stirrups, space at $9''$

We need stirrups at the end face to control spalling cracks

Recall that $.02P$ can be taken as the spalling force: $.02*660 = 13.2 kips$

The 21.6 kip capacity of a #4 stirrup exceeds this $\therefore \text{OK}$

We can use straight #4 bars placed transversely in each flange to resist the force $F_{GH}$

$\frac{39.4}{10.8} = 3.6$ stirrups (note the bar force was not doubled this time, since these are NOT stirrups)

Use 4- #4 bars spaced at $12''$ in each flange