Recall from eq. 1 in Section 2: Strain, that ![]()
Since ![]() ,
, ![]()
or, in index notation:
![]() , since
, since ![]()
and ![]() , by definition.
, by definition.
The tensor, ![]() , is typically referred to as the “deformation gradient.” To see how
, is typically referred to as the “deformation gradient.” To see how ![]() is found in 2D and 3D in an actual FEA application, see Finite Element Coordinate Mapping [McGinty].
is found in 2D and 3D in an actual FEA application, see Finite Element Coordinate Mapping [McGinty].
In matrix form:
(1) 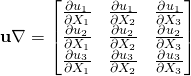
![]() :
:
(2) 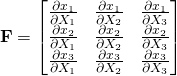
![]() is sometimes called the “stretch” tensor
is sometimes called the “stretch” tensor
Now, consider how the length of any element or fiber within the continuum may change under deformation. To find such length “magnitudes” we can take dot products as follows:
![]() (
(![]() = length
= length ![]() )
)
![]() (
(![]() = length
= length ![]() )
)
![]()
note: you can’t do this transpose manipulation as easily if multiplying two tensors, but it works for two vectors or a vector and a tensor (use indices to easily prove)
![]()
note: ![]() “Right C – G” (Cauchy – Green) deformation tensor. The reason for this name will become clear once we begin discussion our on “polar decomposition” theory.
“Right C – G” (Cauchy – Green) deformation tensor. The reason for this name will become clear once we begin discussion our on “polar decomposition” theory.
(3) ![]()
where the Lagrangian Strain Tensor (or Green-Lagrange Strain Tensor) is: ![]()
or
(4) ![]()
![]() strain vector on a plane whose normal vector is
strain vector on a plane whose normal vector is ![]() (the actual location in space is specified within
(the actual location in space is specified within ![]() )
)
![]() strain (scalar) in direction
strain (scalar) in direction ![]()
note:
From eq. 3, ![]()
Suppose ![]() (infinitesimal deformation):
(infinitesimal deformation):
![]()
i.e. ![]()
what about ![]() ?
?
e.x.
Suppose ![]() and
and ![]() are orthogonal in the undeformed configuration.
are orthogonal in the undeformed configuration.
Since ![]() is the strain vector on a plane whose unit normal is
is the strain vector on a plane whose unit normal is ![]() ,
,
![]() is the component of
is the component of ![]() in direction
in direction ![]() .
.
i.e. if ![]() is in the plane of interest (orthogonal to
is in the plane of interest (orthogonal to ![]() ), then
), then ![]() is the shear strain
is the shear strain

So, ![]()
From eq. 3 and recalling that ![]() , we get:
, we get:
![]()
![]() , where
, where ![]() and
and ![]() are unit vectors
are unit vectors
note: ![]() is “zero” on the LHS of the above equation because
is “zero” on the LHS of the above equation because ![]() and
and ![]() are originally orthogonal
are originally orthogonal
![]()
where ![]() is the “stretch ratio”
is the “stretch ratio”
note: As seen in the figure below, ![]()
![]()
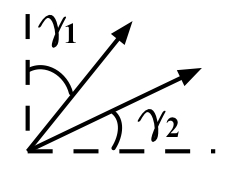
Infinitesimal engineering shear strain =
Does our shear strain reduce to this value for infinitesimal deformation?
For infinitesimal deformation, ![]() ;
; ![]() ;
; ![]()
![]()
![]() for linear infinitesimal deformation
for linear infinitesimal deformation
We can also see from the following equation (eq. 5) that, in general, ![]() for linear infinitesimal deformation (higher order terms are neglected).
for linear infinitesimal deformation (higher order terms are neglected).
For large (“finite”) strain:
(5) ![]()
To prove, first consider: ![]()
![]()
Now, from eq. 3, ![]()
![]()
Recall the definition of ![]() from the figure at the beginning of this chapter, and recall that
from the figure at the beginning of this chapter, and recall that ![]() is the transpose of
is the transpose of ![]()
Eulerian strain:
Here, “Eulerian strain” is simply referring to a measure of strain that is defined in spatial coordinates. Under rigid body rotation, the Eulerian strain values will change, whereas the Lagrangian strain tensor is invariant to rigid body rotation. In other words, the coordinate system in which ![]() is calculated (the “material” coordinate system) rotates with rigid body rotation. The coordinate system in which
is calculated (the “material” coordinate system) rotates with rigid body rotation. The coordinate system in which ![]() is calculated (the “spatial” coordinate system) remains constant.
is calculated (the “spatial” coordinate system) remains constant.
![]()
Similar to the way that we derived ![]() , let’s consider the difference in lengths of any particular element, or fiber, within our strain potato, before and after deformation.
, let’s consider the difference in lengths of any particular element, or fiber, within our strain potato, before and after deformation.
![]()
![]()
where the Eulerian Strain Tensor (sometimes called the Almansi Strain Tensor) is: ![]()
or
(6) ![]()
where ![]() Left C-G Tensor =
Left C-G Tensor = ![]()
![]() , which is easy to prove using indices
, which is easy to prove using indices
![]()
This is analogous to the previously derived ![]()
Proof comes from:
![]()
We’ll see the physical meaning of ![]() and
and ![]() when we discuss “polar decomposition.”
when we discuss “polar decomposition.”
How is ![]() related to
related to ![]() ?
?
![]() ;
; ![]()
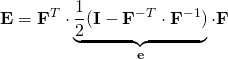
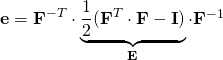
![]()
(To convince yourself that these subscripts are correct, simply write out the matrix multiplication long-hand, summing only the dummy index “k”)
Since ![]() ,
,
![]()
(7) ![]()
If only infinitesimal deformation, and so long as no significant rigid body rotations are present, then ![]()
(this formula may be familiar from undergrad, for example)
