Volume and Area Change

For completeness, we’ll derive the volume change and area change:

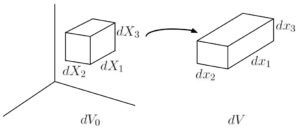
(1) $\begin{equation*} dV=dV_0det\mathbf{F} \end{equation*}$

Derivation starts from the triple scalar product. Cross products and determinants (written in tensor form) is a math topic, so we’ll skip the derivation of volumetric deformation. A quick derivation of volumetric deformation without the use of indices can be found in [Bonet].

note: $det\mathbf{F}=1 \longrightarrow dV=dV_0 \longrightarrow$ “incompressible”

Nanson’s Equation:
Now we know that $dV=(det\mathbf{F})dV_0$ , but what about area?

If $dS_0$ is the initial area and $dS$ is the final area:
For small volumes, we can say that $dV_0=dS_0 \mathbf{dX}$ and $dV=dS \mathbf{dx}$ .

It was previously shown that $dV=det\mathbf{F}dV_0$
$\therefore$ $dV_0=dS_0 \mathbf{dX}$ and $dV=det\mathbf{F}dV_0=dS \mathbf{dx}$ $\longrightarrow dV_0=\frac{dS \mathbf{dx}}{det\mathbf{F}}$

Substituting, we get $dS \mathbf{dx}=dS_0 \mathbf{dX}det\mathbf{F}$
We also know that $\mathbf{dx=F \cdot dX}$

$\longrightarrow \underbrace{dS \mathbf{F}}_{\mathbf{F}^{T}dS} \cdot \mathbf{dX}=dS_0 \mathbf{dX}det\mathbf{F} \longrightarrow (det\mathbf{F}dS_0-\mathbf{F}^{T}dS) \cdot \mathbf{dX}=0$

(2) $\begin{equation*} \longrightarrow dS=dS\mathbf{n}=det\mathbf{F} * \mathbf{F}^{-T}dS_0=det\mathbf{F} * \mathbf{F}^{-T} \cdot \mathbf{N}dS_0 \end{equation*}$

where $\mathbf{N}$ and $\mathbf{n}$ are the normal vectors to the surface in the respective initial and final configurations.

Eq. 2 is called Nanson’s Equation and will be useful later when we look at “true” stress versus “nominal” stress, for example.

J. Bonet and R. Wood, Nonlinear Continuum Mechanics for Finite Element Analysis. 1997, Cambridge University Press, Cambridge.
[Bibtex]

@book{Bonet,
  title={Nonlinear {C}ontinuum {M}echanics for {F}inite {E}lement {A}nalysis. 1997},
  author={Bonet, J and Wood, RD},
  publisher={Cambridge University Press, Cambridge}
}

Leave a Reply Cancel reply