What are the ![]() constants
constants ![]() and
and ![]() ?
?
First, we’ll define the Bulk Modulus “![]() ” by considering a block oriented along the principal strains:
” by considering a block oriented along the principal strains:
Initially, ![]()
After deformation, ![]() ;
; ![]() ;
; ![]()
![]()
![]()
![]() where
where ![]() terms have been eliminated.
terms have been eliminated.
Now, from eq. 4 in Section 8: Linear infinitesimal Elasticity, we know that ![]() can be expressed as follows:
can be expressed as follows:
![]()
Summing both sides on ![]() (and on
(and on ![]() , as always) and noting that
, as always) and noting that 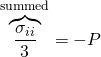 (pressure – e.x. hydrostatic)
(pressure – e.x. hydrostatic)
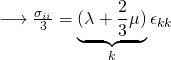
or
![]() , where
, where ![]() = “bulk modulus”
= “bulk modulus”
note:
Next, we’ll define the Young’s Modulus, “![]() ”, the Poisson Ratio, “
”, the Poisson Ratio, “![]() ”, and the shear modulus, “
”, and the shear modulus, “![]() ”. Any two modulii are needed to define an isotropic material (
”. Any two modulii are needed to define an isotropic material (![]() or
or ![]() , etc.)
, etc.)
We need ![]() in terms of
in terms of ![]() ;
;
We’ll start with eq. 4 in Section 8: Linear infinitesimal Elasticity, which is re-written, below:
![]() (1)
(1)
Take the trace:
![]()
![]()
![]()
![]()
![]()
![]() (2)
(2)
(2) ![]() (1) and invert:
(1) and invert:
(1) ![]()
Now we’re ready to find ![]() ,
, ![]() ,
, ![]() :
:
Consider the case of uniaxial tension: 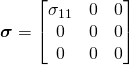
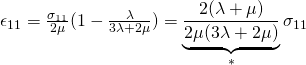
* – must be
(2) ![]()
Now, ![]() ,
,
where ![]() is the lateral strain that occurs from the uniaxial (longitudinal) stress.
is the lateral strain that occurs from the uniaxial (longitudinal) stress.
By definition (i.e. as defined in undergraduate mechanics of materials),
![]()
(3) ![]()
Lastly, consider pure shear: 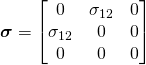
![]()
Since ![]() and
and ![]() (by definition),
(by definition),
(4) ![]()
It can also be easily shown that ![]()
