Any matrix can be decomposed into a sum of symmetric and antisymmetric matrices, but ![]() can be decomposed into a product of two matrices (one symmetric and one orthogonal)
can be decomposed into a product of two matrices (one symmetric and one orthogonal)
(1) ![]()
![]() and
and ![]() are called the Right Stretch Tensor and Left Stretch Tensor due to their respective positions (relative to
are called the Right Stretch Tensor and Left Stretch Tensor due to their respective positions (relative to ![]() ) in eq. 1.
) in eq. 1.
![]() (symmetric)
(symmetric)
![]() (symmetric)
(symmetric)
![]() (orthogonal)
(orthogonal)
A proof of the orthogonality of ![]() is given in Appendix A.3.
is given in Appendix A.3.
(2) ![]()
(3) ![]()
![]() is a rigid body rotation, while
is a rigid body rotation, while ![]() or
or ![]() each stretch and rotate (they each contain both normal and shear deformations, typically)
each stretch and rotate (they each contain both normal and shear deformations, typically)
![]() and
and ![]() have the same eigenvalues. Eigenvalues do not have an “order,” per se, but since
have the same eigenvalues. Eigenvalues do not have an “order,” per se, but since ![]() and
and ![]() typically have different eigenvectors, one should be cautious when assuming equivalency of eigenvalues. In the principal directions of
typically have different eigenvectors, one should be cautious when assuming equivalency of eigenvalues. In the principal directions of ![]() or
or ![]() ,
, ![]() or
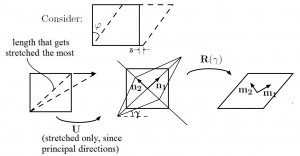
or ![]() contains no shear deformation (see Fig). We’ll look at actual stresses, later.
contains no shear deformation (see Fig). We’ll look at actual stresses, later.
To find the principal directions of ![]() and
and ![]() , we must solve the eigenvalue problem:
, we must solve the eigenvalue problem:
![]()
![]() (pictured)
(pictured)
![]()
![]()
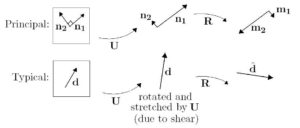
e.x. Polar Decomposition
The deformed equilibrium configuration of a body defined by the deformation mapping:
![]() ,
, ![]() ,
, ![]()
Determine:
a) ![]() and
and ![]()
b) Eigenvalues and eigenvectors of ![]()
c) ![]() and
and ![]()
d) ![]()
e) ![]()
a) ![]() =
= 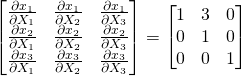
note:
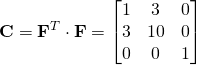
b) ![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]()
![]()
i.e. for ![]() ,
,
![]()
![]()
![]()
Choose arbitrary ![]() ; solve for
; solve for ![]() from either equation ; normalize:
from either equation ; normalize:
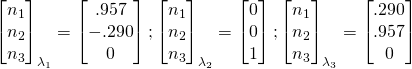
c) ![Rendered by QuickLaTeX.com [\mathbf{U}]_{\mathbf{n}}=\sqrt{[\mathbf{C}]_{\mathbf{n}}}=\begin{bmatrix}\sqrt{\lambda_1} & & \\& \sqrt{\lambda_2} & \\ & & \sqrt{\lambda_3}\end{bmatrix}=\begin{bmatrix}.303 & & \\& 1 & \\ & & 3.303\end{bmatrix}](https://utsv.net/wp-content/ql-cache/quicklatex.com-0a6c942b39e4e7a49ca34592c3095211_l3.png)
![Rendered by QuickLaTeX.com [\mathbf{U}]_{\mathbf{e}}=[\boldsymbol{\Phi}][\mathbf{U}]_{\mathbf{n}}[\boldsymbol{\Phi}]^{T}=\begin{bmatrix} .56 & .83 & 0\\.83 & 3.05 & 0\\0 & 0 & 1\end{bmatrix}](https://utsv.net/wp-content/ql-cache/quicklatex.com-f5920a1e33cb7f75b9e8b599f3b54706_l3.png) (symmetric)
(symmetric)
where ![Rendered by QuickLaTeX.com [\boldsymbol{\Phi}]=\begin{bmatrix} (n_1)_{\lambda_1}&(n_1)_{\lambda_2}&(n_1)_{\lambda_3} \\(n_2)_{\lambda_1}&(n_2)_{\lambda_2}&(n_2)_{\lambda_3} \\ (n_3)_{\lambda_1}&(n_3)_{\lambda_2}&(n_3)_{\lambda_3} \end{bmatrix}](https://utsv.net/wp-content/ql-cache/quicklatex.com-1276f0c084a045a2f899a123b458a089_l3.png)
It’s important to keep in mind that ![]() ,
, ![]() , and
, and ![]() have the same eigenvectors and that these eigenvectors (and any other strain direction or magnitude) are generally dependent on the particular point in space of interest (e.g.
have the same eigenvectors and that these eigenvectors (and any other strain direction or magnitude) are generally dependent on the particular point in space of interest (e.g. ![]() ,
, ![]() ,
, ![]() ). For this simple example,
). For this simple example, ![]() is independent of
is independent of ![]() ,
, ![]() , and
, and ![]() (i.e. the deformation is the same everywhere in the body – a “homogenous” deformation), but this would generally not be the case.
(i.e. the deformation is the same everywhere in the body – a “homogenous” deformation), but this would generally not be the case.
The eigenvalues occur in the direction of the eigenvectors, thus, ![]() ;
; ![]() ;
; ![]() . It makes sense that if we only know the eigenvectors and want to undo this transformation to bring us back to
. It makes sense that if we only know the eigenvectors and want to undo this transformation to bring us back to ![]() , then we need a transformation matrix that involves
, then we need a transformation matrix that involves ![]() . We can see that
. We can see that ![]() is the opposite of the usual
is the opposite of the usual ![]() , and without going through the rigorous derivation of why
, and without going through the rigorous derivation of why ![]() ,
, ![]() ,
, ![]() , it at least makes some sense intuitively.
, it at least makes some sense intuitively.
d) ![Rendered by QuickLaTeX.com [\mathbf{R}]_{\mathbf{e}}=[\mathbf{F}]_{\mathbf{e}}[\mathbf{U}]_{\mathbf{e}}^{T}=\begin{bmatrix} .55 & .83 & 0\\ -.83 & .55 & 0\\0 & 0 & 1\end{bmatrix}](https://utsv.net/wp-content/ql-cache/quicklatex.com-305b8a2ed2a91a7a42187b9095416a31_l3.png) (orthogonal ;
(orthogonal ; ![]()
e) ![Rendered by QuickLaTeX.com [\mathbf{V}]_{\mathbf{e}}=[\mathbf{F}]_{\mathbf{e}}[\mathbf{R}]_{\mathbf{e}}^{T}=\begin{bmatrix}3.05 & .83 & 0\\.83 & .55 & 0\\0 & 0 & 1\end{bmatrix}](https://utsv.net/wp-content/ql-cache/quicklatex.com-ae26c42d62a251719d794b93d80cb97f_l3.png)
