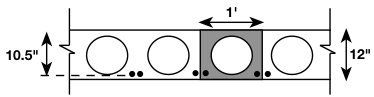
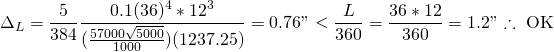9. Slab Design Example

Post-tensioned, un-bonded one-way slab with draped tendons (midspan moments will be assumed to control)

$A = \frac{262}{4} = 65.5in^2$ , where $262in^2$ is the area of the entire section shown above and $65.5in^2$ is the shaded area.
$I = \frac{4949}{4} = 1237.25in^4$ , which is the moment of inertia of the shaded area
$e = 10.5 - 6 = 4.5''$
c = 6”
$f'_c = 5000 psi$
$f'_{ci} = 3500 psi$
$f_{pu} = 270 ksi$ , low-relaxation $(f_p = 0.75f_{pu})$

$LL = 100 psf$
$DSL = 10 psf$
$\frac{L}{h} = 37$

Friction, anchor set, long-term losses

A detailed friction analysis could be performed, as done in an earlier section, but here we will just estimate $f_{pi}$ as $187 ksi$ , and $f_{pe}$ as $157 ksi$ .

Finding $A_ps$

member self-weight $= 150*\frac{262in^2}{4}*\frac{1}{144} = 68 plf$ (per foot width)

$SDL = 10 psf * 1' = 10 plf$ (per foot width)

$LL = 100 psf * 1' = 100 plf$ (per foot width)

$M_{max} = (0.68 + 0.010 + 0.100)*\frac{36^2}{8} = 28 ft*kips$ (per foor width, working stress)

$e + k_t = 4.5" + \frac{S_b}{A} = 4.5 + \frac{1237.25/6}{65.5} = 7.65"$

$6\sqrt{f'_c} = 424psi$

(1) $\begin{equation*} P_f \geq \frac{(28ft*kips*12 ) - (\frac{1237.2}{6})(0.424)}{7.65} = 32.5 kips \text{(per foot width)} \end{equation*}$

Note: this is based on bottom tension at service

$A_{ps} \geq \frac{32.5 kips}{153 ksi} = 0.212 in^2$ (per foot width)

Also, for strength,

$M_{max} = [1.2*(0.068+0.01) + 1.6*0.100]\frac{36^2}{8} = 41 kip*ft$ (per foot width, LRFD)

$A_{ps} \geq \frac{41*12}{0.77*270*12" = h} = 0.197 in^2$

Try two $\frac{1}{2}''$ diameter strands; $A_{ps} = 2*0.153 = 0.306 in^2$ (per foot width)

Check top tension at transfer

$3\sqrt{3500} = 177 psi$

(2) $\begin{equation*} e \leq k_b + \frac{M_{min} + S_tf_t}{P_i}\end{equation*}$

where $M_{min} = (0.068) \frac{36^2}{8} = 11.1kip*ft$ , $P_i = 183ksi*0.306 = 56 kips$ ,

$S_t = S_b = \frac{1237.25}{6} = 206.2in^3, k_b = \frac{S_t}{A} = \frac{(\frac{1237.25}{6})}{65.5} = 3.15 in$

(3) $\begin{equation*} e \leq 3.15 + \frac{(11.1*12) + (206.2)(0.177)}{56} = 6.18 in > 4.5 in \therefore \text{ OK}\end{equation*}$

Check bottom compression at transfer

$\frac{-P_i}{A} = -855 psi$

$\frac{-P_ie}{S_b} = -1222 psi$

$\frac{M_{min}}{S_b} = 646 psi$

$\Sigma = -1431 psi < 0.6f'_{ci} = 2100 psi \therefore \text{ OK}$

Check top compression service

$\frac{P_f}{A} = \frac{-153*0.306*1000}{65.5} = -715 psi$

$\frac{P_fe}{S_t} = 1022 psi$

$\frac{-M_{max}}{S_t} = -1629 psi$

$\Sigma = -1322 psi <0.45f'_c = 2250 psi \therefore \text{ OK}$

Code specified minimum mild steel in slab

$A_s = 0.004*\frac{65.5}{2} = 0.131in^2$ (per foot width)

Choose one #4 bar per foot $(d \cong d_p = 10.5")$

$A_s = 0.2in^2$ (per foot width)

Strength

For members with unbonded tendons:

For members with span-to-depth ratios of 35 or less,

(4) $\begin{equation*} f_{ps} = f_{pe} + 10000 + \frac{f'_c}{100\rho_p}, \text{ psi (empirical)}\end{equation*}$

Else,

(5) $\begin{equation*}f_{ps} = f_{pe} + 10000 + \frac{f'_c}{300\rho_p}, \text{ psi} \end{equation*}$

where $\rho_p = \frac{A_{ps}}{bd_p}$

For our example,

$\frac{L}{h} = 36$

$f_{ps} = 153000 + 10000 + \frac{5000}{300\rho_p}, \rho_p = \frac{0.306}{(12)(10.5)} = 0.0024$

$f_{ps} = 169.9 ksi$

There are two checks:

$169.9 < 0.9(270) = 243$ and $<153 + 30 = 183 \therefore \text { OK}$

(6) $\begin{equation*} \omega = \frac{A_s}{bd}\frac{f_y}{f'_c} = \frac{0.2}{(12)(10.5)}\frac{60}{5} = 0.019\end{equation*}$

(7) $\begin{equation*} \omega_p = \frac{A_{ps}}{bd_p}\frac{f_{ps}}{f'_c} = \frac{0.306}{(12)(10.5}\frac{169.9}{5} = 0.0825 \end{equation*}$

(8) $\begin{equation*} \omega_p + \frac{d}{d_p}\omega = 0.0825 + \frac{10.5}{10.5}(0.019) = 0.1 < 0.36(0.8) = 0.288 \therefore \text{ OK} \end{equation*}$

(9) $\begin{equation*} \beta_1 = 0.85 - (f'_c - 4000)(0.00005) = 0.8 \geq 0.65 \end{equation*}$

(10) $\begin{equation*} a = \frac{A_{ps}f_{ps}}{\gamma f'_cb} = \frac{(0.306)(169.9)}{(0.85)(5)(12)} = 1.02" < ~ 1.5" \Rightarrow \text {the n.a. is below the hollow portion}\end{equation*}$

(11) $\begin{equation*} \phi M_n = 0.9[A_{ps}f_{ps}(d_p - \frac{a}{2}) + A_sf_y(d-\frac{a}{2})] = 575kip*in = 47.9kip*ft \text { (per foot width)} > 41 kip*ft \therefore \text{ OK} \end{equation*}$

Check Ductility

$7.5\sqrt{f'_c} = 530 psi$

$530 = -\frac{P_f}{A} - \frac{P_fe}{S_b} + \frac{M_{cr}}{S_b} = -715 psi - 1022 psi + \frac{M_{cr}}{206.2} \Rightarrow M_{cr} = 467 kip*in$

(12) $\begin{equation*} \frac{\phi M_n}{M_{cr}} = \frac{575}{467} = 1.23 > 1.2 \therefore \text{ OK} \end{equation*}$

Quick deflection check

(13) $\begin{equation*} \Delta_L = \frac{5}{384} \frac{0.1(36)^4*12^3}{(\frac{57000\sqrt{5000}}{1000})(1237.25)}= 0.76" < \frac{L}{360} = \frac{36*12}{360} = 1.2" \therefore \text{ OK} \end{equation*}$