Typically, the equation of motion is solved in small increments of time, and the constitutive relationships are developed in rate form. “Rate” formulation in structural analysis is useful even if the actual “rates” involved are small or negligible, since incremental time stepping in time allows one to keep track of parameters that may be history dependent. This is the case, for example, in plasticity. At the other end of the spectrum, we may have a purely elastic problem, but one in which the rates are high enough that material parameters change (strain rate effects on stiffness). This cannot be considered unless we formulate our equations in rate form! These are merely examples that are meant to convey the importance of rates. Neither plasticity (metals), viscoelasticity (polymers), nor general rate effects (any material) will be considered in this text.
The rate form for hyperelastic materials, which forms the basis for the material modeling of rubber, require a special “hypoelastic” treatment. We will consider this in a later chapter. Furthermore, we will see that in linear infinitesimal elasticity, where the basic constitutive relationship is relatively simple, one has to still carefully consider factors such as change of reference frame due to rigid body rotations. Incremental or rate formulations handle such issues quite nicely.
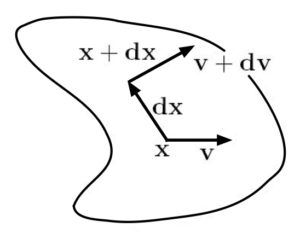
The velocity at a point in the continuum, similar to the displacement at a point, depends on both position and time:
![]()
![]()
