8. Beam Design Example

Rules of Thumb:

Preliminary choice of section depth: $h = \frac{L}{25}$

Note: the method outlined in the previous section on ‘Required Section Moduli’ is more precise, albeit more cumbersome. A rule-of-thumb is typically used in practice.

Preliminary choice of $A_{ps}$ is based on ultimate strength: $0.77*A_{ps}f_{pu}h = \frac{w_uL^2}{8}$

Note: the working stress method outlined previously did not take into account ultimate strength.

Ultimate strength analysis, as well as deflection analysis, will be included in the examples to follow.

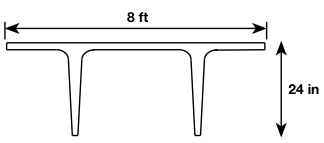
Double-Tee, pretensioned, floor member (simply supported)

$f'_c = 5000 psi$
$f_{pu} = 270 ksi$ , low-relaxation $(f_p=0.75f_{pu})$
Concrete strength at transfer, $f'_{ci} = 3500 psi \Rightarrow f_{ci} = 0.6f'_{ci} = 2100 psi$

$L = 46'$
$LL = 50 psf$
$SDL = 15 psf$

A $24"$ beam would have a span-to-depth ratio of about $23$ . We can try the following section:

note: The previous procedure used a much more complicated approach for choosing a section size. While that approach may be optimal for a simply supported beam or an I-shape (where moment reversal is not an issue due to the symmetry of the section shape), the previous approach is generally viewed as being overly complicated. Additionally, deflections were certainly not considered in the previous procedure, whereas this rule-of-thumb is based on practical experience, with consideration of deflections.

$A = 401 in^2$
$I = 20985 in^4$
$S_b = 1224 in^3$
$S_t = 3063 in^3$

$DL = 418 plf$
$SDL = 15psf* 8 ft = 120 plf$
$LL = 50 psf*8 ft = 400 plf$

Preliminary design (based on final stage, midspan stresses):

(1) $\begin{equation*} M_{max} = (.418 + .120 + .400)\frac{46^2}{8} = 248 ft*kips \end{equation*}$

(2) $\begin{equation*} M_{u} = [1.4(.418 + .120) + 1.7(.400)]\frac{46^2}{8} = 379ft*kips \end{equation*}$

Note: load factors may vary depending on the code that is used

$e + k_t \approx 0.7h$ (from the table in the previous section)

Note: this is not as accurate as our previous example, since $0.70h$ is just an approximation

$0.70h = 0.70*24 = 16.8in$

$\therefore e+k_t \approx 16.8 in$

Also, we can solve for $e$ : $e = 13.75in$

$6\sqrt{f'_c} = 6\sqrt{5000} = 424 psi$

(3) $\begin{equation*} P_f \geq \frac{M_{max} - S_bf_b}{e+k_t} = \frac{248*12 - 1224*.424}{16.8} = 146 kips\end{equation*}$

If we were looking at the intermediate stage, as we did for the previous example, then we would be using the inequality [ $P_i \leq$ expression].

In our earlier example, we essentially found $e$ and $P_i$ from optimizing stresses at the intermediate stage (larger $e$ and/or $P_i$ would cause simultaneous crushing and cracking at the intermediate stage).

Essentially, here, we’ve found $e$ and $P_f$ , by optimizing the bottom stress at the final stage (a smaller $e$ and/or $P_f$ would cause tensile cracking at the final stage). Crushing is not considered. However, for a T-beam, it is probably satisfactory to neglect crushing under service loads, since it is so unlikely due to the relatively large compression flange.

For low-relaxation strands, stressed to $0.75f_pu, f_{pi} = 187 ksi$ and $f_{pf} = 157 ksi$

$A_{ps} \geq \frac{146 kips}{157 ksi} = 0.93in^2$

In addition, rule-of-thumb:

$M_u = \phi M_n = 0.77A_{ps}f_{pu}h$

$0.77A_{ps}f_{pu}h \geq 379 ft*kips$

$A_{ps} \geq \frac{379*12}{0.77*270*24} = 0.91in^2$

Use six $\frac{1}{2} in$ strands for $A_{ps} = 6*0.153 = 0.92in$

Check of intermediate stage, midspan:

$3\sqrt{3500} = 177 psi$

$e \leq k_b + \frac{M_{min} + S_tf_t}{P_i}$

$M_{min} = 1327in*kips$

$P_i = A_{ps}f_{pi} = 0.92*187 = 172 kips$ (the 187ksi accounts for immediate losses, such as elastic shortening; some codes may use 189ksi)

$e \leq 7.64 + \frac{1327 + 3063(.177)}{172} = 18.5"$

Any larger, and the top face would crack in tension at the intermediate stage (crushing is not considered).

Our $13.75 in$ eccentricity, found earlier from $e + k_t = 0.70h$ , is less than this value. In fact, we can increase this value to $14.65in$ , which is the full depth of the beam minus $2.5in$ cover.

Note: We will assume that the tendons are harped, with an “ $e$ ” of about $9''$ at the support.

Note: The previous example had calculated $e$ and $A_{ps}$ based on the initial condition, and then checked the final condition. Here, we did the opposite: we calculated $e$ and $A_{ps}$ based on the final condition, and then checked the initial condition. This is not the only difference between the two methods. Firstly, for the first method, if the required section modulii equations were used, then the final condition would not actually need to be checked. The fact that the stress capacities would exceed demands at the final condition would have been implied. Secondly, checks to ensure that stress demands fall below both the crushing and the cracking limits, are also implied, for the first method. For the latter method, only cracking has been considered.

So far, we’ve only looked at midspan. At other locations, $M_{min}$ and $M_{max}$ differ (both will be smaller in this case), so these other locations need to be checked.

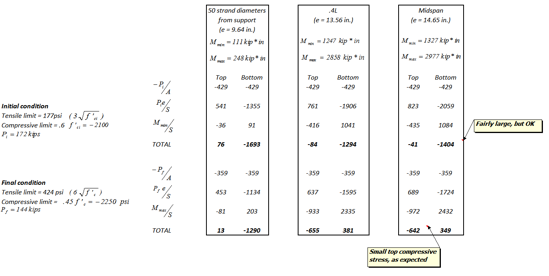
We’ve also neglected crushing so far, which is probably not a satisfactory assumption for the transfer stage, where the compression will be in the web of the T-beam. Thus, we will check the stresses (both tensile and compressive) at midspan as well, which includes compression.

The following table shows the concrete stresses, in units of psi:

Ultimate strength check:

For pretensioned members or post-tensioned with bonded tendons (empirically derived):

(4) $\begin{equation*} f_{ps} = f_{pu}(1-\frac{\gamma_p}{\beta_1}[\rho_p\frac{f_{pi}}{f'_c} + \frac{d}{d_p}(\omega -\omega')])\end{equation*}$

Recall $\beta_1$ from the following equation:

$\beta_1 = 0.85(f'_c \leq 4000 psi)$

$\beta_1 = 0.85 - (f'_c - 4000)*.00005 \geq 0.65 (f'_c > 4000 psi)$

$\gamma_p = 0.4$ for stress-relieved strands

$\gamma_p = 0.28$ for low-relaxation strands

$\rho_p = \frac{A_{ps}}{bd_p}$

If mild reinforcement is present:

$d$ and $d_p$ are the distances from the extreme compression fiber to the centroid of the mild reinforcement and to the centroid of the prestressing steel, respectively

$\omega = \frac{\rho f_y}{f'_c}$ and $\omega' = \frac{\rho' f_y}{f'_c}$

Additional constraints:

$[\rho_p \frac{f_{pu}}{f'_c} + \frac{d}{d_p}(\omega - \omega')] \leq 0.17$ , if compression reinforcement is accounted for.

If $d'$ is greater than $0.15d_p$ , then $\omega' = 0$ .

So, back to our example problem, assuming no mild reinforcing:

(5) $\begin{equation*} f_{ps} = 270(1-\frac{0.28}{0.80}*\frac{0.92}{8ft*12\frac{in}{ft}*21.5in}*\frac{270}{5}) = 268 ksi\end{equation*}$

Note: additional check:

(6) $\begin{equation*} \omega_p = \frac{A_{ps}f_{ps}}{bd_pf'_c} = \frac{0.92*268}{96*21.5*5} = 0.025 < 0.36*\beta_1 = 0.36*0.80 = 2.88 \therefore \text { OK} \end{equation*}$

Now we will find the ultimate moment capacity exactly as done in ordinary reinforced concrete:

(7) $\begin{equation*} a = \frac{A_{ps}f_{ps}}{0.85f'_cb} = 0.60"\end{equation*}$

(8) $\begin{equation*} \phi M_n = \phi A_{ps}f_{ps}(d_p - \frac{a}{2}) = 0.9*0.92*268*(21.5 - \frac{0.60}{2}) = 4460 kip*in = 392 kip*ft \end{equation*}$

This is greater than $M_u = 379 kip*ft \therefore \text{ OK}$

There is an additional ‘ductility’ check which relates $M_u$ to $M_{cr}$ :

We need to calculate $M_{cr}$ , which is not a small value and can be calculated as follows:

We can take a realistic concrete tensile strength to be $7.5\sqrt{f'_c} = 530 psi$

Note from the above table of working stress demands for our beam, that the tensile stress at the bottom fiber, at midspan, under final conditions, is $349 psi$ .

Hence, to cause cracking, an additional tensile stress of $530 - 349 = 181 psi$ , is needed.

Hence, an additional moment of $S_b*.181 = 222 kip*in$ would be needed, on top of the moment of $2977 kip*in$ from service load. This results in a total moment of $3199 kip*in$ to crack the beam. Now we can check that our ultimate moment capacity is significantly greater than this value, in an attempt to ensure under-reinforced behavior.

(9) $\begin{equation*} \frac{\phi M_n}{M_{cr}} = \frac{392kip*ft*12\frac{in}{ft}}{3199kip*in} = 1.47 > 1.20 \therefore \text{ OK} \end{equation*}$

Deflections:

Multipliers for estimating long-term cambers and deflections

	Composite	Non-composite
At transfer:
Deflection from member self-weight	1.85	1.85
Camber from prestressing	1.80	1.80
At final stage:
Deflection from member self-weight	2.70	2.40
Camber from prestressing	2.45	2.20
Deflection from superimposed DL and 30% LL	3.00	3.00

a) Immediate deflection due to LL:

$E_c = 57000 \sqrt{f'_c} = 57000\sqrt{5000} = 4031ksi$

$\Delta_L = \frac{5wL^4}{384EI} = 0.48"$ , where $w = 0.400 klf$ (Live Load)

This is less than $\frac{L}{360} = 1.53" \therefore \text{OK}$

b) Check deflections likely to damage partitions

We will assume non-composite construction for this example.

To calculate the deflection that will affect partitions, we must first estimate the deflection of the member at the time that the partitions are attached:

$E_c = 57000\sqrt{3500} = 3372 ksi$

$\Delta = \frac{5wL^4}{384EI} = 0.60"$ , where $w = .418 klf$ (self weight)

Note:

For a single harping point, $\Delta_{up} = \frac{2e_{min} + e_{sup}}{24}\frac{PL^2}{EI}$

For a draped tendon, $\Delta_{up} = \frac{5PeL^2}{48EI}$

We will assume a single harping point here:

(10) $\begin{equation*} \Delta = - \left(\frac{2*14.65 + 9}{24}\right)\left(\frac{172*46^2*144}{3372*20985}\right) = -1.19" \text{(PT)}\end{equation*}$

Now, we need to account for a small amount of creep during erection time, so we use the multipliers in the above table:

$\Delta = 1.85*0.60 - 1.80*1.19 = -1.03"$ (upward)

This is the deflection of the member at the time that the partitions are attached.

$\Delta = \frac{5wL^4}{384EI} = 0.34"$ , where $w = (SDL + 0.3LL) = 0.120 + 0.3*0.400 plf$

The long term deflection =

def due to self-weight + def due to PT + def due to $SDL+.3LL$ , with each of these three terms being multiplied by appropriate factors from the above table to account for long term creep and relaxation:

$\Delta = 2.70*0.60 - 2.45*1.19 + 3.00*.34 = -.28''$ (upward)

Note: we could’ve used $P_f$ rather than $P_i$ , but these values are already conservative enough, since we’re using a very low $E$ value based on $f_{ci}$ .

So, the long-term deflection that occurs after the attachment of partitions, is:

$-.28 - (-1.03) = .75''$ (downward)

At any point in time, there could be the addition of the rest of the live load, causing an additional immediate deflection of:

$\Delta = 70\%*\Delta_L = 0.70*0.48 = 0.34"$ , where $\Delta_L$ was calculated in part ‘a’

Thus, the total deflection that would cause the partitions to potentially crack, is:

$\Delta = 0.75" + 0.34" = 1.09"$

(Strict limit for deflection sensitive parts)

$L/480 = 1.15" \therefore \text{OK}$

Rather than using the multipliers in the table, creep coefficients could have been used, as was done in the ‘deflections’ section, for ordinary reinforced concrete.