Rate of Deformation and Spin Tensors

The most obvious first step is to take the time derivative of the deformation gradient, $\mathbf{F}$ , as follows:

$\dot{\mathbf{F}}=\frac{d}{dt}\frac{\partial\mathbf{x}}{\partial\mathbf{X}}=\frac{\partial}{\partial\mathbf{X}}\left(\frac{d\mathbf{x}}{dt}\right)=\frac{\partial}{\partial\mathbf{X}}\mathbf{v}$

For reasons that won’t become clear until the chapter on rate-form constitutive expressions, we would like the “velocity gradient” to be expressed with respect to $\mathbf{x}$ rather than $\mathbf{X}$ . Since $\mathbf{x}$ is a function of $\mathbf{X}$ , we can use the chain rule to arrive at the following important expression:

(1) $\begin{equation*} \dot{\mathbf{F}}=\frac{\partial}{\partial\mathbf{X}}\mathbf{v}=\underbrace{\frac{\partial\mathbf{v}}{\partial\mathbf{x}}}_{\mathbf{L}}\underbrace{\frac{\partial\mathbf{x}}{\partial\mathbf{X}}}_{\mathbf{F}} \end{equation*}$

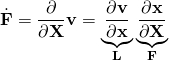
We can see from eq. 1 that $\mathbf{\dot{F}}=\mathbf{L \cdot F}$
or
$\mathbf{L}=\mathbf{\dot{F}} \cdot \mathbf{F}^{-1}$ , where $\mathbf{L}$ is the “velocity gradient.”

For our purposes, consider that if we were to have analytical functions of time, $t$ , for each term in $\mathbf{F}$ that describes how $\mathbf{R}$ and $\mathbf{U}$ are changing with time, for example, then we could find $\mathbf{L}$ by noting that $\dot{\mathbf{F}}=\frac{d}{dt}\left(\mathbf{R\cdot U}\right)=\dot{\mathbf{R}}\cdot\mathbf{U}+\mathbf{U}\cdot\dot{\mathbf{R}}$ and $\mathbf{L}=\mathbf{\dot{F}} \cdot \mathbf{F}^{-1}$ . This is quite academic (and potentially quite difficult) compared to the way that $\mathbf{L}$ would be found in FEA, so such an example will not be given. However, $\mathbf{L}$ is a very important quantity as we will see in the chapter on rate-form constitutive relationships.

The velocity gradient, $\mathbf{L}$ , is a very important quantity and can be decomposed as follows:

(2) $\begin{equation*} \mathbf{L}=\underbrace{\frac{1}{2}(\mathbf{L+L}^{T})}_{\mathbf{D}}+\underbrace{\frac{1}{2}(\mathbf{L-L}^{T})}_{\mathbf{W}} \end{equation*}$

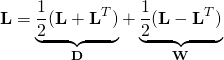
note: Similar to eq. 2, in linear infinitesimal elasticity, we can split the displacement gradient into a strain tensor and rotation tensor that are symmetric and anti-symmetric, respectively.

note: Any tensor can be similarly split into its symmetric and anti-symmetric parts.

“Rate of Deformation Tensor” = symmetric $\longrightarrow \mathbf{D}^{T}=\mathbf{D}$
“Spin Tensor” = anti-symmetric or “skew” $\longrightarrow \mathbf{W}^{T}=-\mathbf{W}$

$\mathbf{W}$ is a pure rigid body rotation. A complete proof of this can be found in [Asaro]. It can also be easily shown that $\mathbf{W}$ is, in fact, skew. This proof can be found in Appendix A.2.

Consider the time rate of change of length of a particular element:
$\frac{d}{dt}(ds)^2=\frac{d}{dt}(\mathbf{dx \cdot dx})=\frac{d}{dt}(\mathbf{dX \cdot F}^{T} \cdot \mathbf{F \cdot dX})=\mathbf{dX \cdot}\frac{d}{dt}(\mathbf{F}^{T} \cdot \mathbf{F})\cdot \mathbf{dX}$
$=\mathbf{dX \cdot \dot{C} \cdot dX}$

$\frac{d\mathbf{C}}{dt}=\mathbf{\dot{C}}=(\dot{\mathbf{F}^{T} \cdot \mathbf{F}})=\dot{\mathbf{F}}^{T} \cdot \mathbf{F} + \mathbf{F}^{T} \cdot \dot{\mathbf{F}}=\mathbf{F}^{T} \cdot (\dot{\mathbf{F}} \cdot \mathbf{F}^{-1}+\mathbf{F}^{-T} \cdot \dot{\mathbf{F}}^{T}) \cdot \mathbf{F}$
$=\mathbf{F}^{T} \cdot (\mathbf{L+L}^{T})\cdot \mathbf{F}=2 \cdot \mathbf{F}^{T} \cdot \mathbf{D \cdot F}$

So, $\frac{d}{dt}(ds)^2=2\mathbf{dX \cdot F}^{T} \cdot \mathbf{D \cdot F \cdot dX}=2\mathbf{dx \cdot D \cdot dx}$

$\mathbf{dx}=ds\mathbf{n} \longrightarrow \frac{d}{dt}(ds)^2=\cancel{2(ds)}\frac{d}{dt}(ds)=\cancel{2}(ds)^{\cancel{2}}\mathbf{n \cdot D \cdot n}$

(3) $\begin{equation*} \longrightarrow \frac{d}{dt}(ds)=D_{nn}ds \end{equation*}$

While [Holzapfel] shows that “ $\mathbf{D}$ is not pure rate of strain and $\mathbf{W}$ is not a pure rate of rotation,” we can see that the rate of change of length only depends on $\mathbf{D}$ , not $\mathbf{W}$ . Additionally, if $\mathbf{D}=0,$ then we must have rigid body motions only.

note: We could have split up $\mathbf{F}$ into a sum, but we wouldn’t have arrived at anything useful. The way that eq. 3 was derived only works due to the product rule of derivatives. Proving that $\mathbf{W}$ represents “spin” is more difficult and won’t be shown here, although the derivation can be found in many other texts (e.x. [Asaro][Bonet][Holzapfel]).

Similar to the shear strain, $E_{mn}$ , we can again consider how the angle between two vectors, $\mathbf{m}$ , and $\mathbf{n}$ , changes under deformation (see Fig below).

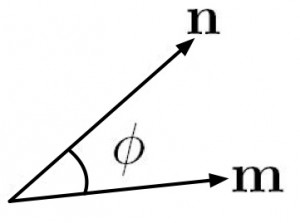
(4) $\begin{equation*} \frac{d\phi}{dt}=2D_{mn}\text{ (skipped work)} \end{equation*}$

note: $\mathbf{\dot{E}}=\mathbf{F}^{T} \cdot \mathbf{D \cdot F}$ (Recall also: $\mathbf{E}=\mathbf{F}^{T} \cdot \mathbf{e \cdot F}$ )
$\mathbf{\dot{E}}$ reduces to $\mathbf{D}$ for infinitesimal deformation (ignoring rigid body rotations), since $\mathbf{F \longrightarrow I}$ .
In general, though, $\mathbf{\dot{E}} \ne \mathbf{\dot{e}} \ne \mathbf{D}$ . Similarly, in general, $\mathbf{\dot{R}} \ne \mathbf{W}$ . We’ll also look in detail at the physical meaning (or lack thereof) of $\boldsymbol{\dot{\sigma}}$ later on when we get to the chapter on “Rate-Form Constitutive Expressions”

R. J. Asaro and V. A. Lubarda, Mechanics of Solids and Materials, Cambridge, UK: Cambridge University Press, 2006.
[Bibtex]

@BOOK{Asaro,
    Address        = {Cambridge, UK},
    Author         = {Robert J. Asaro and Vlado A. Lubarda},
    Edition        = {},
    Publisher      = {Cambridge University Press},
    Title          = {Mechanics of Solids and Materials},
    Year           = {2006}
}

G. Holzapfel, Nonlinear Solid Mechanics, John Wiley & Sons Ltd., England, 2000.
[Bibtex]

@book{Holzapfel,
  title={Nonlinear Solid Mechanics},
  author={Holzapfel, GA},
  year={2000},
  publisher={John Wiley \& Sons Ltd., England}
}

J. Bonet and R. Wood, Nonlinear Continuum Mechanics for Finite Element Analysis. 1997, Cambridge University Press, Cambridge.
[Bibtex]

@book{Bonet,
  title={Nonlinear {C}ontinuum {M}echanics for {F}inite {E}lement {A}nalysis. 1997},
  author={Bonet, J and Wood, RD},
  publisher={Cambridge University Press, Cambridge}
}

Leave a Reply Cancel reply