In preparation for the constitutive formulations in later chapters, this short chapter will derive how different tensors behave under superimposed rigid body motion. This will enable us, for example, to show that ![]() is a function of
is a function of ![]() in the beginning of the next chapter. The idea of “work conjugate” pairs will be introduced in this chapter. We will see that the Cauchy stress tensor,
in the beginning of the next chapter. The idea of “work conjugate” pairs will be introduced in this chapter. We will see that the Cauchy stress tensor, ![]() , for example, changes with rigid body rotation, while
, for example, changes with rigid body rotation, while ![]() does not. Thus,
does not. Thus, ![]() and
and ![]() are not work-conjugate, and therefore it would not be appropriate to use them as a pair when forming a constitutive relationship. This was first recognized by Hill [Hill].
are not work-conjugate, and therefore it would not be appropriate to use them as a pair when forming a constitutive relationship. This was first recognized by Hill [Hill].
Let’s define the vector ![]() as follows:
as follows:
![]() , where
, where ![]() is a superimposed rigid body motion, sometimes called a Euclidean transformation (see Fig).
is a superimposed rigid body motion, sometimes called a Euclidean transformation (see Fig).
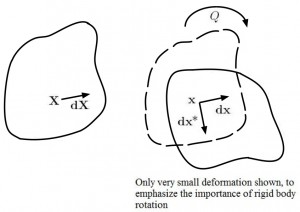
We know that ![]()
What about “![]() ”?
”?
Consider the following square body (see Fig), paying careful attention to the heavily bolded edge in order to track the motion of the body.
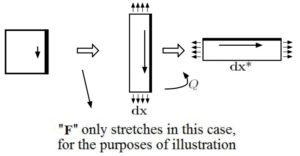
Clearly, if ![]() (which is what we’re going to want), and, say,
(which is what we’re going to want), and, say, ![]() ,
,
then ![]() (this should be clear from the above Fig).
(this should be clear from the above Fig).
Since we want to find ![]() such that
such that ![]() , we can conclude that
, we can conclude that ![]() .
.
What we do know is the following:
![]() ;
; ![]() ;
; ![]()
So, ![]() , which gives:
, which gives:
(1) ![]()
Eq. 1 is what we wanted to find, and it should be expected. Recall that ![]() is physically understood to be a deformation (axial strains and shear),
is physically understood to be a deformation (axial strains and shear), ![]() , followed by a rotation,
, followed by a rotation, ![]() . Thus,
. Thus, ![]() is the total deformation + rotation,
is the total deformation + rotation, ![]() , followed by an explicit rigid body rotation,
, followed by an explicit rigid body rotation, ![]() , – i.e. a rotation that is superimposed on
, – i.e. a rotation that is superimposed on ![]() .
.
Now, we can see how different measures of strain and stress behave under superimposed rigid body motion, by substituting the above expression for ![]() .
.
(2) ![]()
Thus, ![]() is invariant to rigid body motion.
is invariant to rigid body motion.
note:
note:
informal proof:
or
![]() NOT =
NOT = ![]() which does not match either of the above expressions for
which does not match either of the above expressions for ![]()
(or ![]() which is similarly
which is similarly ![]() )
)
![]()
![]() matches
matches ![]() expression for
expression for ![]()
or
![]()
![]() matches
matches ![]() expression for
expression for ![]()
formal proof: see Appendix A.1
(3) ![]()
What about ![]() ,
, ![]() , and
, and ![]() ?
?
![]()
![]()
![]()
Recall, ![]()
Insert ![]() into the above expression
into the above expression ![]()
So, ![]() ;
; ![]() (
(![]() is symmetric ;
is symmetric ; ![]() is orthogonal)
is orthogonal)
Also, ![]() (skipped work)
(skipped work)
How about rates?
![]()
Recall also, ![]()
So, ![]()
note: (
(4) ![]()
note:
How about stress?
Since ![]() , we can say that
, we can say that ![]() (1)
(1)
We also know the following three expressions to be true:
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
(4) ![]() (1)
(1) ![]() (3)
(3) ![]()
![]() (5)
(5)
(2) ![]() (5)
(5) ![]() (
(![]() )
)![]()
(5) ![]()
note: Since
How about the nominal stress and the Second Piola-Kirchhoff Stress?
![]()
Again, we will need to use ![]()
Since ![]() depends on
depends on ![]() , we will need
, we will need ![]() . It turns out, though, that
. It turns out, though, that ![]()
note: the determinant of an orthogonal tensor is “1”
So, ![]()
![]()
![]()
How about ![]() ?
?
![]()
![]()
(6) ![]()
![]() is a good measure of stress when there are small (infinitesimal) strains. It will also be used as a “work-conjugate pair” with
is a good measure of stress when there are small (infinitesimal) strains. It will also be used as a “work-conjugate pair” with ![]() in the following chapters on constitutive relationships.
in the following chapters on constitutive relationships.
- G. A. Holzapfel, Nonlinear Solid Mechanics: A Continuum Approach for Engineering, Baffins Lane, Chichester, West Sussex PO19 1UD, England: John Wiley & Sons Ltd., 2000.
[Bibtex]@book{holzapfel, address = {Baffins Lane, Chichester, West Sussex PO19 1UD, England}, author = {Holzapfel, Gerhard A.}, publisher = {John Wiley \& Sons Ltd.}, title = {{Nonlinear Solid Mechanics: A Continuum Approach for Engineering}}, year = {2000} } - R. Hill, “On constitutive inequalities for simple materials I,” Journal of the Mechanics and Physics of Solids, vol. 16, iss. 4, pp. 229-242, 1968.
[Bibtex]@article{Hill, title={On constitutive inequalities for simple materials I}, author={Hill, R}, journal={Journal of the Mechanics and Physics of Solids}, volume={16}, number={4}, pages={229--242}, year={1968}, publisher={Elsevier} }
