Pre-tensioned fasteners

Consider the figure below, which shows a bolt under pre-tension.

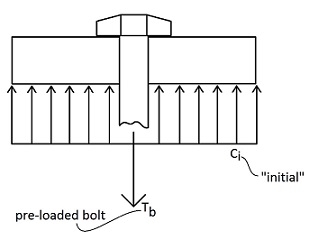
The bolt is pre-loaded to a tension $T_b$ , and the plate(s) is pre-loaded to a compression $C_i$ .

The lengthening of the bolt under this pre-tension is:

$\begin{equation*} (\delta_i)_{bolt} = \frac{T_b L_b}{A_b E_b} \end{equation*}$

The shortening of the plate (or in many cases, multiple plates) under this pre-compression is:

$\begin{equation*} (\delta_i)_{plate}=\frac{C_i t_p}{A_p E_p} \end{equation*}$

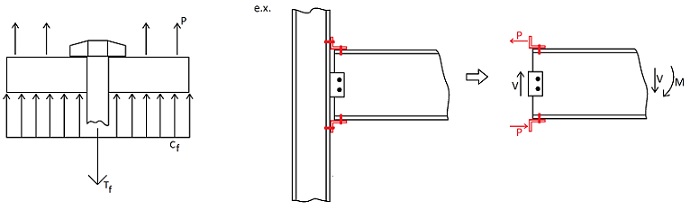
The figure below shows the loads on the bolt and plate after an external force is applied. In the figure, the example that is shown is a moment connection that uses angles instead of welds. Under application of a beam moment, each leg of each angle is pulled in a way that causes some additional tension in the bolt and some reduction in compression of the plate. This force that’s applied to the connection assembly is denoted $P$ in the figure. What we’ll prove is that only a small fraction of this force, $P$ , causes additional tension in the bolt, so long as the bolt has been sufficiently pre-tensioned.

First, let’s look at the additional lengthening of the bolt, in terms of the force $T_f$ , which is so far unknown.

$(\delta_f)_{bolt} = (\delta_i)_{bolt} + \delta_{add} = \frac{T_b L_b}{A_b E_b} + \delta_{add}$

$\rightarrow \delta_{add}=(\delta_f)_{bolt} - \frac{T_b L_b}{A_b E_b}$

(1) $\begin{equation*} \delta_{add}=\frac{T_f L_b}{A_b E_b} - \frac{T_b L_b}{A_b Eb} \end{equation*}$

Now, let’s look at the lengthening of the plate(s), which is written in terms of unknown variables $C_i$ and $C_f$ .

$(\delta_f)_{plate}=(\delta_i)_{plate} - \delta_{decrease}=\frac{C_i t_p}{A_p E_p} -\delta_{decrease}$

$\rightarrow \delta_{decrease} = \frac{C_i t_p}{A_p E_p} - (\delta_f)_{plate}$

(2) $\begin{equation*} \delta_{decrease}=\frac{C_i t_p}{A_p E_p} - \frac{C_f t_p}{A_p E_p} \end{equation*}$

We’d like to find an expression that relates $T_f$ to $T_b$ and $P$ . In other words, we’d like to know how the pre-load in the bolt, $T_b$ , affects the final tension in the bolt, $T_f$ , when the connection assembly is subjected to external tensile loads, $P$ . We currently have two equations and many “unknowns” ( $\delta_{add}$ , $\delta_{decrease}$ , $C_i$ , $C_f$ , $T_f$ ). We need to consider force equilibrium and displacement compatibility in order to solve.

Since the bolts and the plates “lengthen” by the same amount:

(3) $\begin{equation*} \delta_{add} = \delta_{decrease} \end{equation*}$

From equilibrium of our two free-body diagrams (prev. figures that contain $T_b$ , $C_i$ , and $T_f$ , $C_f$ , $P$ ), we have two additional equations:

(4) $\begin{equation*} C_i = T_b \end{equation*}$

(5) $\begin{equation*} P+C_f=T_f \end{equation*}$

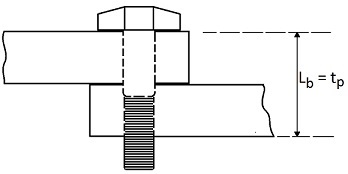
We can see in the above figure that:

$\begin{equation*} L_b = t_p \end{equation*}$

Additionally, we can assume that the bolt and the plate have the same $E$ (they are both steel), so that:

$\begin{equation*} E_b = E_p \end{equation*}$

We now have $5$ equations (1 2 3 4 5) and $5$ unknowns ( $\delta_{add}$ , $\delta_{decrease}$ , $C_i$ , $C_f$ , $T_f$ ), so we can solve for the desired result ( $T_f$ expressed in terms of $T_b$ and $P$ ):

(6) $\begin{equation*} T_f = T_b + \frac{P}{1+ A_p/A_b} \end{equation*}$

From eq. 6, we can conclude that only a small fraction of the load “ $P$ ” is actually “added” to the bolt, so long as a) the plate is big and b) the bolt has been sufficiently pre-tensioned so that the bolt and plate remain in contact when “ $P$ ” is applied. Eq. 6 would not be applicable if the bolt is not sufficiently pre-tensioned (e.x. $T_f$ would simply be equal to $P$ , if $T_b$ is zero).

Pre-tensioned bolts have a relatively constant tension, even if the external loading (i.e. “ $P$ ”) is cyclical. This relatively constant tension is necessary to avoid bolt failure due to fatigue.

C. G. Salmon and J. E. Johnson, Steel Structures: Design and Behavior, 5th ed., New York, NY: Prentice Hall, 2008.
[Bibtex]

@BOOK{Salmon,
    Address        = {New York, NY},
    Author         = {Charles G. Salmon and John E. Johnson},
    Edition        = {5th},
    Publisher      = {Prentice Hall},
    Title          = {Steel Structures: Design and Behavior},
    Year           = {2008}
}

Leave a Reply Cancel reply