For completeness, we’ll quickly derive the rate of volume change and the rate of area change:
Volume:
If ![]() , where
, where ![]() ,
, ![]() ,
, ![]() are the lengths of the sides of a “box” that is oriented in the principal directions of
are the lengths of the sides of a “box” that is oriented in the principal directions of ![]() , then:
, then:
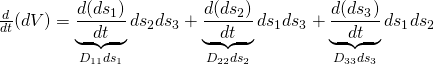
(1) ![]()
Area:
Consider the following time derivative:
![]()
where ![]() is an area (as opposed to
is an area (as opposed to ![]() ,
, ![]() ,
, ![]() , which are lengths).
, which are lengths).
![]() is known from eq. 2 in Section 2: Volume and Area Change. So, we can take the time derivative. We can also re-write
is known from eq. 2 in Section 2: Volume and Area Change. So, we can take the time derivative. We can also re-write ![]() in terms of
in terms of ![]() .
.
(2) 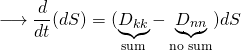
The derivation was skipped here, but can be found in [Holzapfel].
We’ll come back to rates again when we get to rate-form constitutive relationships.
- G. Holzapfel, Nonlinear Solid Mechanics, John Wiley & Sons Ltd., England, 2000.
[Bibtex]@book{Holzapfel, title={Nonlinear Solid Mechanics}, author={Holzapfel, GA}, year={2000}, publisher={John Wiley \& Sons Ltd., England} }
