Recall that ![]() and
and ![]() were shown to be work-conjugate, and this permitted us to develop a constitutive relationship between the two tensors. Now we would like to develop a constitutive relationship in hypoelastic form. Thus, we need a stress rate and a strain rate that are work-conjugate. Unfortunately, the time derivative of the Cauchy stress tensor,
were shown to be work-conjugate, and this permitted us to develop a constitutive relationship between the two tensors. Now we would like to develop a constitutive relationship in hypoelastic form. Thus, we need a stress rate and a strain rate that are work-conjugate. Unfortunately, the time derivative of the Cauchy stress tensor, ![]() , is not work-conjugate with
, is not work-conjugate with ![]() , where we recall that
, where we recall that ![]() is the “rate of deformation tensor.” Consider the following:
is the “rate of deformation tensor.” Consider the following:
(1) ![]()
Here, ![]() is the “Truesdell rate.” Essentially, we wrote
is the “Truesdell rate.” Essentially, we wrote ![]() in terms of the Second Piola-Kirchhoff Stress, and then, within this expression, we took the time derivative of only the Second Piola-Kirchhoff Stress (recall from eq. 2 in Section 4: Alternative Measures of Stress, that the Second-Piola Kirchhoff Stress,
in terms of the Second Piola-Kirchhoff Stress, and then, within this expression, we took the time derivative of only the Second Piola-Kirchhoff Stress (recall from eq. 2 in Section 4: Alternative Measures of Stress, that the Second-Piola Kirchhoff Stress, ![]() , is
, is ![]() ).
).
The time derivative expressed in eq. 1 can be taken, which requires the use of the product rule for the four terms within the square brackets. An alternative derivation is given in Appendix D.2. In either case, eq. 1 becomes:
(2) ![]()
Recall the definition of the velocity gradient, ![]() , from eq. 1 in Section 3: Rate of Deformation and Spin Tensors. Additionally, note that
, from eq. 1 in Section 3: Rate of Deformation and Spin Tensors. Additionally, note that ![]() .
.
Eq. 2 is the most commonly used form of the Truesdell rate. In eq. 2, if we eliminate all of the ![]() terms except for those that appear in the constitutive relationship (we can also think of this simplification as taking
terms except for those that appear in the constitutive relationship (we can also think of this simplification as taking ![]() ), then we arrive at the following result:
), then we arrive at the following result:
(3) ![]()
or
(4) ![]()
note:
In hypoelasticity, eq. 3 is called the Jaumann rate of Cauchy Stress. We will form our hypoelastic constitutive relationship in terms of this rate. Then, we’ll see how this constitutive relationship would be used to solve real FEA problems, through a simple three step time-stepping algorithm. But first, we need to prove that the Jaumann rate of Cauchy Stress is indeed work conjugate with ![]() – i.e. does
– i.e. does ![]() ?
?
Note that
Recall ![]()
![]()
![]()
![]()
Since ![]()
![]()
Moving some of the terms to the other side:
![]()
Since ![]()
and ![]()
![]()
Since we know that ![]()
(5) ![]()
Note the similarity to
Now, just as we have derived ![]() in the past, we can now derive
in the past, we can now derive ![]() (
(![]() will also depend on
will also depend on ![]() ,
, ![]() , and
, and ![]() ).
).
Truesdell et al. [Truesdell] coined the phrase “hypoelasticity.” All hyperelastic constitutive relationships can be put into rate form (and hence are hypoelastic). The reverse is not always possible [Simo]. Materials that are viscoelastic, or any material that is expected to experience plasticity, can be conveniently expressed in rate form, where history dependent variables can be tracked, naturally.
note:
Since all of the tensors above are work-conjugate, it is convenient to use them to derive our final form of ![]() .
.
Recall ![]() :
:
We will form our hypoelastic constitutive relationship by applying the Jaumann “operator” (![]() ) to both sides of this expression. But, before we do this, we ought to find
) to both sides of this expression. But, before we do this, we ought to find ![]() and
and ![]() .
.
![]() (i.e. presumably, the analog to
(i.e. presumably, the analog to ![]() would simply be zero, since any asymmetries cancel out when taking the determinant)
would simply be zero, since any asymmetries cancel out when taking the determinant)
From eq. 1 in Section 2: Volume and Area Change we know that ![]() and from eq. 1 in Section 3: Other Rates of Change we know that
and from eq. 1 in Section 3: Other Rates of Change we know that ![]() .
.
So, ![]() . Thus,
. Thus,
(6) 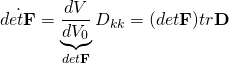
In terms of ![]() :
: ![]()
Next, we need to find ![]() :
:
![]()
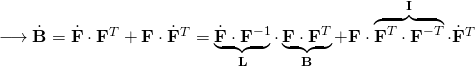
![]()
![]() , (since
, (since ![]()
and ![]() )
)
![]()
Reminder: The direct calculation of the time derivative of
![]() | apply the Jaumann operator (
| apply the Jaumann operator (![]() ) to this entire expression.
) to this entire expression.
Noting that 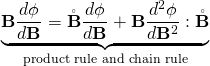
![]()
note: Recall from Section Section 1. Trace, Scalar Product, Eigenvalues that
So, ![]()
where ![]() :
:
![]()
Since ![]() , all terms in the above expression involve
, all terms in the above expression involve ![]() . Thus, we arrive at the following relationship:
. Thus, we arrive at the following relationship:
(7) ![]()
Eq. 7 is the Jaumann rate of Cauchy Stress in terms of deformation, stress, and rate of deformation.
Note that we could’ve formed a slightly different hypoelastic relationship using the Truesdell rate. Either way, the hypoelastic expression is going to be complicated (the Truesdell rate, slightly more so). This is, however, meant to be broad enough to treat materials that are both nonlinear elastic, and subjected to large strain.
- C. Truesdell and W. Noll, The Non-Linear Field Theories of Mechanics, 3rd ed., Berlin, DE: Pringer, 2004.
[Bibtex]@BOOK{Truesdell, Address = {Berlin, DE}, Author = {Clifford Truesdell and Walter Noll}, Edition = {3rd}, Publisher = {Pringer}, Title = {The Non-Linear Field Theories of Mechanics}, Year = {2004} } - G. A. Holzapfel, Nonlinear Solid Mechanics: A Continuum Approach for Engineering, Baffins Lane, Chichester, West Sussex PO19 1UD, England: John Wiley & Sons Ltd., 2000.
[Bibtex]@book{holzapfel, address = {Baffins Lane, Chichester, West Sussex PO19 1UD, England}, author = {Holzapfel, Gerhard A.}, publisher = {John Wiley \& Sons Ltd.}, title = {{Nonlinear Solid Mechanics: A Continuum Approach for Engineering}}, year = {2000} } - J. C. Simo and T. J. R. Hughes, Computational inelasticity, Springer, 1998.
[Bibtex]@book{hughes, title={Computational inelasticity}, author={Simo, J.C. and Hughes, T.J.R.}, Publisher = {Springer}, year={1998} } - G. Jaumann, “Geschlossenes System physikalischer und chemischer Differentialgesetze,” Sitzungsberichte Akad. Wiss. Wien, IIa, pp. 385-530, 1911.
[Bibtex]@article{Jaumann, title={Geschlossenes {S}ystem physikalischer und chemischer {D}ifferentialgesetze}, author={Jaumann, Gustav}, journal={Sitzungsberichte Akad. Wiss. Wien, IIa}, pages={385--530}, year={1911} }
